Начнем с того, что эта статья окончательно разубедит тех, кто думает, что шифровать – это просто. Даже в том случае, когда в распоряжении имеются надежные криптографические инструменты, можно легко споткнуться о подводные камни при использовании их на практике. Одному из таких "камней" и посвящена настоящая статья. Речь пойдет об особенностях использования некоторых механизмов симметричной криптографии, а именно о недолговечности симметричного ключа.

Существование каких-либо особенностей на практике не означает, что используемые схемы не надежны. В теории надежность или стойкость криптографических схем определяется только в совокупности с условиями, в которых та или иная схема должна функционировать (они определяют возможности потенциального противника). Задача тех, кто данные схемы использует на практике, – сделать реальные условия максимально близкими к "безопасным" теоретическим условиям. Так, априорное существование общих методов и подходов, позволяющих компрометировать ключ или данные при наличии у противника большого объема информации, приводит к появлению таких важных понятий, как "нагрузка на ключ" и "срок жизни ключа". В настоящей статье мы рассмотрим проблему недолговечности симметричного ключа и расскажем о существующих подходах к ее решению.

Что скрывается за словосочетанием "шифрование данных"?

С тех пор, как криптография выделилась в самостоятельный раздел науки, ее терминологическая база активно расширяется (блочные шифры, режимы работы шифра, нагрузка на ключ, срок жизни ключа, механизм смены ключа), что может вносить путаницу и усложнять понимание.  Ситуация в отечественной криптографии усугубляется еще и неточностью перевода, так как большинство терминов заимствуются из английского языка. В настоящей статье мы будем говорить только о криптографических конструкциях, основанных на блочных шифрах, и далее коротко введем необходимые для этого понятия и поясним связь между ними.

Примитивы — это математические объекты, которые сами по себе не позволяют решать какие-либо прикладные задачи криптографии. Примерами являются хэш-функция, группа точек эллиптической кривой, блочный шифр. Поговорим о последнем. Блочный шифр (или просто шифр) — семейство взаимно однозначных отображений множества двоичных строк некоторой фиксированной длины (блоков) в себя, индексируемое ключом, который тоже является двоичной строкой фиксированной длины. Блочный шифр оперирует исключительно с блоками, то есть абстрактной единицей его работы является блок. Примерами блочных шифров являются алгоритмы Магма и Кузнечик, определяемые в ГОСТ Р 34.12-2015.

Утверждение "данные зашифрованы с помощью блочного шифра" не в полной мере описывает состояние дел, потому что зашифровать с помощью любого шифра можно по-разному — стойко и не стойко. Например, шифровать каждый блок по отдельности — плохая идея. В этот момент возникает такое понятие, как режим работы шифра — порядок применения шифра для обработки сообщения, размер которого может не только превышать размер блока, но и не быть кратным ему. Режимы шифрования проектируются таким образом, чтобы минимально зависеть от принципов работы самого шифра (максимум, от размеров блока и ключа). Единицей работы режима является уже не блок, а целое сообщение. Все режимы разрабатываются для решения конкретных прикладных задач — обеспечения конфиденциальности или целостности, причем разные режимы могут решать разные задачи. Например, конфиденциальность информации обеспечивают такие режимы шифрования, как CTR, OFB, CFB, CBC. В свою очередь, для обеспечения целостности используются режимы выработки кода аутентификации OMAC, TMAC, CBC-MAC. Также существуют режимы, решающие одновременно обе задачи: GCM, CCM (так называемые режимы аутентифицированного шифрования (AEAD)). Описание некоторых из этих режимов можно найти в ГОСТ Р 34.13-2015.

Теперь о криптографических свойствах описанных объектов. Понятие стойкости определяется в рамках модели противника и не существует отдельно от понятия угрозы. Чтобы не нагружать читателя введением сложных определений, не нужных для понимания основной идеи статьи, под "стойкостью" будем подразумевать отсутствие у противника какой-либо возможности компрометировать ключ или данные.

Итак, фундамент заложен и можно переходить к обсуждению основной темы статьи.

Может ли ключ "жить" вечно?

Рассмотрим следующую прикладную задачу. Пусть нам необходимо на протяжении многих лет обмениваться с кем-то информацией, каждый фрагмент которой после передачи месяц хранится в секрете, после чего публикуется. 

Для начала согласуем общий секретный ключ, например, при личной встрече в защищенном от прослушивания подземном бункере. Насколько длинным он должен быть? Всем известно, что ключ можно найти с помощью полного перебора, но перебрать, например, 2²⁵⁶ возможных значений 256-битного ключа даже за 1000 лет невозможно. Таким образом, 256 бит должно хватить на очень долгое время. Далее выбираем стойкий блочный шифр с соответствующей длиной ключа, а также стойкий режим шифрования.

Можно начинать работу. Данные передаются, все идет хорошо. 

По прошествии всего нескольких месяцев мы понимаем, что кто-то явно читает нашу переписку, при этом в совокупности нами было передано чуть больше 5 терабайт данных. В чем может быть причина? А причина в том, что мы не обратили внимания на размер блока используемого шифра, который оказался слишком мал - всего 40 битов (2⁴⁰ значений блоков • 5 байтов в блоке = 5 терабайтов). Противник терпеливо собирал передаваемые по каналу зашифрованные данные и соответствующие им открытые тексты, которые публиковались через месяц после передачи. С помощью собранных данных он в конце концов узнал результаты применения используемого блочного шифра ко всем возможным блокам и сохранил эти результаты в таблицу. Таким образом, с ее помощью он смог расшифровывать любые данные, не зная ключ.

Этот простой пример демонстрирует важность условий, в которых функционирует система защиты информации, а именно важность учета так называемой нагрузки на ключ.  Нагрузка на ключ — это объем данных, обработанных на одном ключе. В рамках настоящей статьи будем считать, что нагрузка на ключ измеряется в блоках.

Практика показывает, что обработка большого количества сообщений на одном ключе может привести к потере стойкости (к компрометации ключа, дешифрованию конфиденциальных сообщений). В примере, описанном выше, противник использовал фундаментальное свойство блочного шифра — взаимную однозначность отображений, приводящую к тривиальному ограничению нагрузки на ключ порядка 2ⁿ, где n – длина блока. Однако существуют другие не столь очевидные классы методов, необходимым условием работы которых также является наличие у противника большого объема данных:

1. Методы анализа, основанные на свойствах используемого шифра 
   Наиболее распространёнными методами это типа являются линейный и дифференциальный методы. Для "хороших" блочных шифров данные методы требуют наличия материала, объем которого по порядку соответствует тривиальному ограничению 2ⁿ. В данной статье мы исходим из того, что используемый шифр стойкий, и поэтому не будем далее учитывать эти ограничения. 
2. Методы анализа, основанные на комбинаторных свойствах используемого режима работы шифра
   Как уже было сказано ранее, комбинаторные свойства режимов минимально зависят от особенностей внутреннего строения используемого блочного шифра. Эти свойства начинают проявляться при обработке большого количества данных и могут привести к появлению реальных угроз. Ярким примером метода, осуществляющего такие угрозы, является атака Sweet32 на TLS, приводящая к частичному дешифрованию трафика. Ограничения, обусловленные методами этого типа, будем для краткости называть комбинаторными ограничениями (для большинства режимов по порядку они равны 2^n/2).
3. Методы, основанные на информации, полученной по побочным каналам
   При функционировании криптографических систем на практике у противника появляются возможности, которых нет на бумаге, — он может получать информацию о секретных параметрах системы с помощью так называемых побочных каналов. К ним можно отнести энергопотребление, электромагнитное излучение, акустический шум, время работы алгоритма. При обработке большого количества сообщений "опасная" информация, полученная по побочным каналам, накапливается, что может привести к осуществлению реальных угроз, например, вскрытию ключа.  Примером метода, осуществляющего такие угрозы, является атака TEMPEST, также теме атак по побочным каналам посвящена одна из предыдущих статей нашего блога. Ограничения, обусловленные методами такого рода, будем называть ограничениями по побочным каналам.

Примечание: ограничения, соответствующие методам анализа из пункта 1, близки к тривиальному 2ⁿ (в силу стойкости блочного шифра) и далее не рассматриваются. Также в рамках данной статьи будем считать, что ограничения по побочным каналам гораздо более сильные, чем комбинаторные (что обычно соответствует реальному положению дел).  

Итак, после рассмотрения такого обилия различных методов становится очевидно, что ограничивать нагрузку на ключ не только желательно, но и необходимо. Отсюда возникает такое понятие как допустимая нагрузка на ключ или срок жизни ключа (в английском языке используется термин key lifetime) — объем данных, который можно "безопасно" обработать на одном ключе. Здесь под словом "безопасно" также будем понимать отсутствие у противника возможности компрометировать любую конфиденциальную информацию.

Что если данных очень много?

Конкретное значение допустимой нагрузки на ключ определяется протоколом, в рамках которого используется тот или иной шифр и режим шифрования, с учетом описанных выше методов анализа и необходимого уровня стойкости.

Рассмотрим такой протокол. Исходя из необходимого уровня стойкости протокола фиксируется допустимая нагрузка на ключ L. Предположим, что на одном ключе обрабатывается q сообщений. Для упрощения понимания будем предполагать, что все сообщения имеют одинаковую длину m блоков.  Параметры q и m должны выбираться так, чтобы суммарный размер этих сообщений не превосходил допустимую нагрузку на ключ, т.е.  q•m ≤ L. Графически это можно изобразить следующим образом: допустимая нагрузка на ключ L ограничивает площадь прямоугольника высоты q и длины m:

 

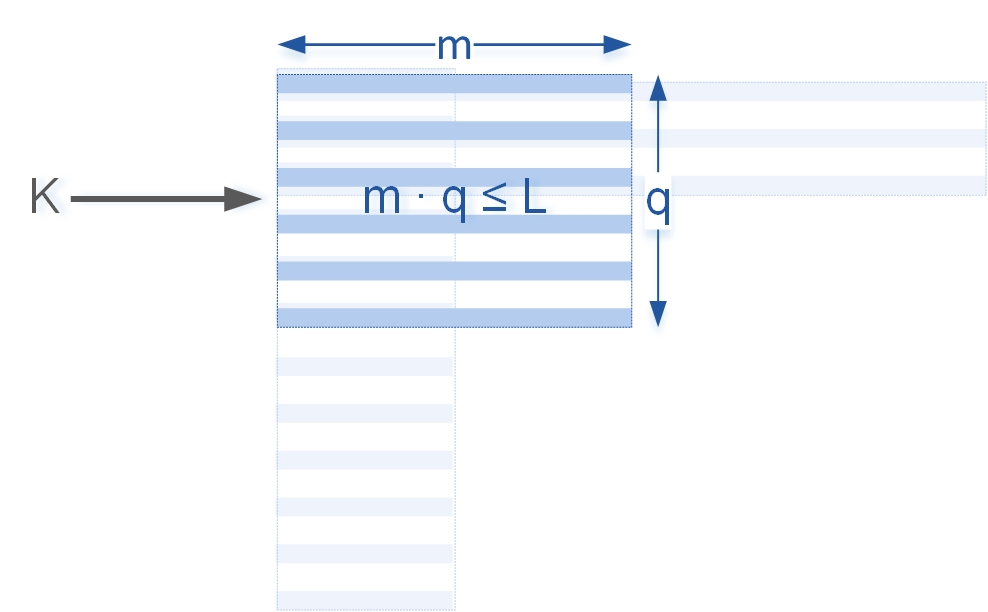
Следовательно, если хочется обрабатывать сообщения большей длины, придется обрабатывать меньшее количество сообщений, и, напротив, при обработке большого числа сообщений, все они должны быть небольшого размера. На практике часто бывает, что допустимая нагрузка на ключ оказывается слишком мала и с помощью одного ключа удается обработать очень небольшое число сообщений ограниченной длины. Но что делать, если нужно обрабатывать больше данных, не теряя стойкости?

Естественным решением проблемы "безопасной" обработки большого объема данных, которое первым приходит в голову, является замена ключа на новый по истечении срока его жизни. Казалось бы, все просто: шифруем максимально возможный объем данных, заменяем старый ключ на новый, и продолжаем в том же духе. Такая "замена" в протоколах обычно называется пересогласованием ключа. Однако у такого подхода есть существенный недостаток: низкая эффективность. В большинстве протоколов пересогласование ключа приведет к прекращению передачи прикладных данных, пересылкам ряда служебных сообщений, работе датчика случайных чисел и вообще уйме дополнительных вычислений, а в некоторых случаях придется задействовать крайне ресурсоемкую асимметричную криптографию.

Неужели не существует эффективного способа решения данной проблемы? К счастью, такой способ есть, и известен он под названием re-keying (преобразование ключа). О нем, его особенностях и разновидностях будет рассказано в следующей части нашей статьи.

 

 

 

 

Смышляев С.В., к.ф.-м.н.,

начальник отдела защиты информации

ООО "КРИПТО-ПРО"

Алексеев Е.К., к.ф.-м.н.,

ведущий инженер-аналитик

ООО "КРИПТО-ПРО"

 

Смышляева Е.С.,

инженер-аналитик 2 категории

ООО "КРИПТО-ПРО"

 

Мешков Д.А.,

студент 4-го курса

МИЭМ НИУ ВШЭ